It is known that Net Pay is a key parameter in reservoir evaluation and is central to the volumetric method of estimating ultimate hydrocarbon recovery. Many algorithms have been developed since 1984 by geoscientists to estimate net pay, among which, Seismic Net Pay (SNP) implements a set of algorithms to accurately estimate the net pay between two seismic picks made on zero-crossings of band-limited impedance data. SNP is also developed along with uncertainty estimation.
Extended Elastic Impedance (EEI) technology, Colored Inversion (CI) and Power Law geology models are the phenomenological bases of SNP algorithms. EEI theory provides a method to increase the correlation of the impedance profile with a reservoir property (Neves et al, 2004), which simplifies and improves the accuracy of the net pay estimation process. CI shapes the spectrum of the seismic data to have the same "colour" as the geology within the seismic bandwidth. Coloured Inversion data can be modeled as a flat-topped trapezoidal wavelet convolved with an impedance profile. The use of CI data allows SNP to model the tuning response more easily than by reflectivity methods. Furthermore power law geology models are now available to provide more realistic synthetic data sets to assess the accuracy and optimise the algorithms of SNP.
SNP algorithms are based on measuring two interval attributes, Average Band Limited Impedance vs Time Thickness (LH chart below), and Seismic Net-to-Gross vs Time (RH chart below) to derive a detuning transform. This has shown to be more accurate than techniques that use amplitude measurements taken from two reflecting boundaries. The attribute measurements are taken from a band-limited impedance wedge created by applying a trapezoidal filter to a low impedance wedge model (see Wedge model chart below). The acoustic impedance model should be convolved with a wavelet that is consistent with the spectral characteristics of the coloured inversion operator. The SNP algorithms are based on the observation of a proportional correlation between average band-limited impedance and net-to-gross when pay thickness is not larger than a half cycle of the lowest frequency component of the wavelet.
Figure 2.1. Wedge model with a wavelet convolution
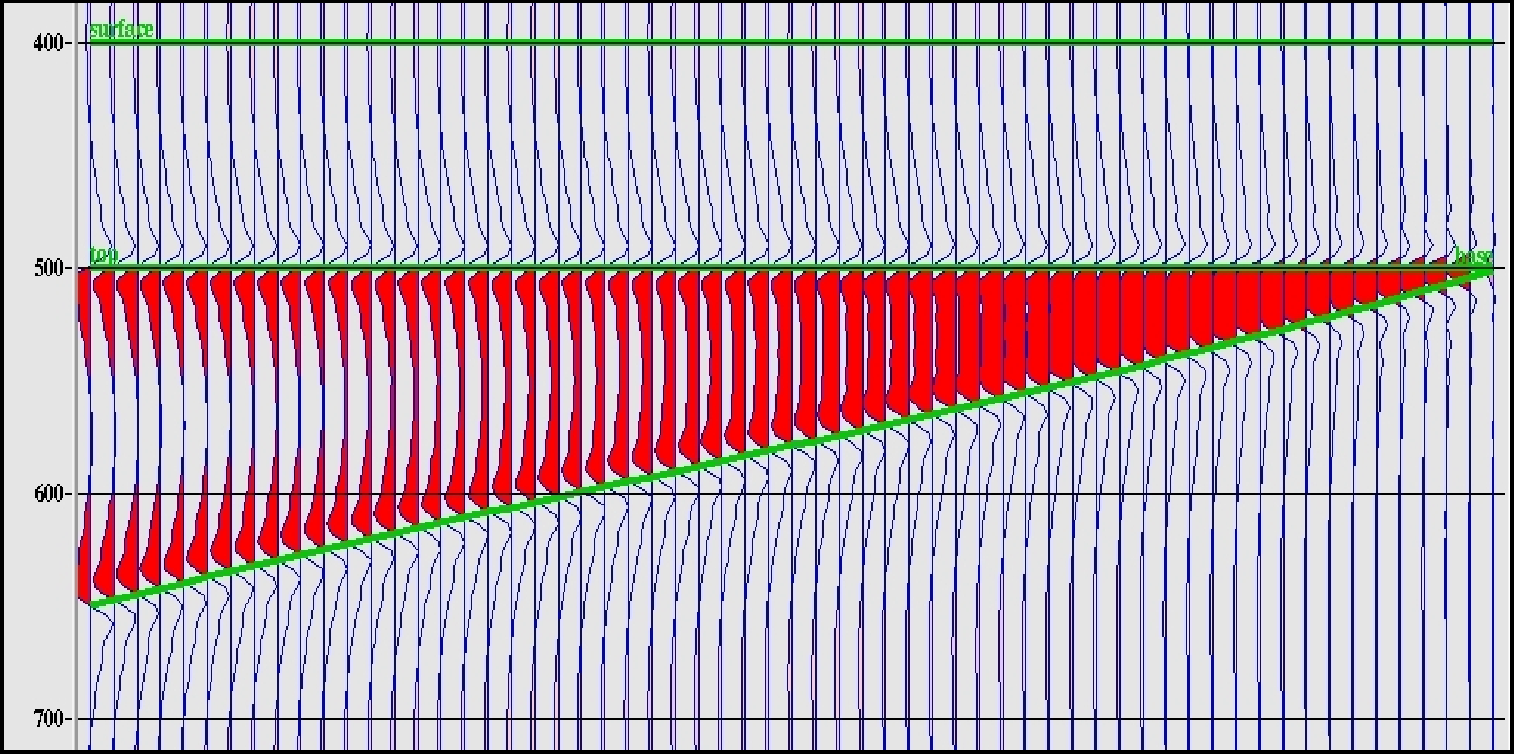 |
The diagram above shows a wedge model with a wavelet convolution with a varying boxcar impedance profile.
Figure 2.2. Average Amplitude and Net to Gross
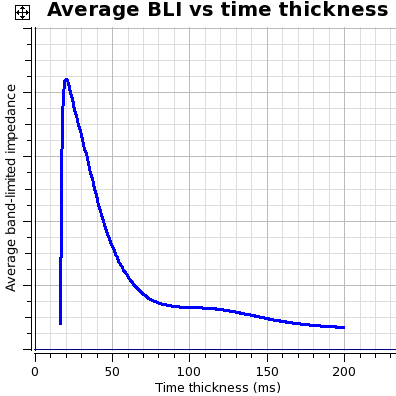 | .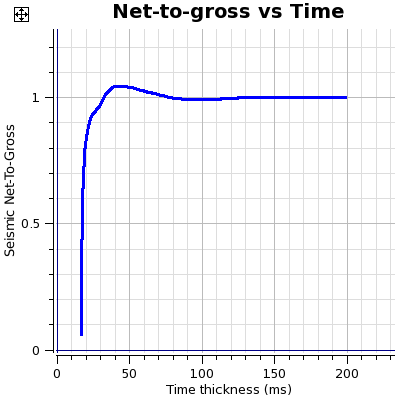 |
The chart on the left shows Average band-limited impedance versus gross time thickness. The chart on the right shows Seismic net-to-gross for 100% net-to-gross wedge model versus gross time thickness.
Statistical analysis of the performance of SNP algorithms has been carried out by using a Monte Carlo approach to generate synthetic data sets. Extensive tests on real data sets have also been done based on binary-impedance models, which show that the SNP method is more accurate than any other attribute based technique and can give reliable results for a wide range of conditions. It has been proved that the SNP based band-limited impedance technique is a significant improvement on the reflectivity based techniques, and others, in terms of simple amplitude-scaling techniques for net pay estimation from the seismic.
SNP has two major steps, detuning and calibrating, which can be separately carried out with a fairly small number of parameters. The methods of calibration optimisation are well defined and implemented in SNP through wavelet specification, self-calibration and well calibrations. Each process step has been modularized and can be carried out independently in multiple runs if necessary. SNP algorithms are robust, the uncertainties are well estimated and presented in a user-friendly manner.